Mathe und Info

Seite

CI81 - M

ACHTUNG: Diese Inhalte werden ab sofort nicht weiter gepflegt. Ab sofort befinden sich sämtliche Inhalte zu diesem Kurs in Logineo, der offiziellen Lernplattform des Berufskolleg Technik Remscheid.

Einfach auf das Logo klicken und Ihr werdet zu der Login Seite geführt.

oder alternativ hier klicken:

externer Link: [Logineo: offizielles Lernmanagement System des BTR]

hier findet ihr die gesammelten Aufgaben des Schuljahres (neueste oben, älteste unten)

Inhalte des vorhergehenden Schuljahres findet ihr hier [Link zum Schuljahr 2019/2020]

in blau das Veröffentlichkeitsdatum
in grün das Abgabedatum

CI81 - M Vektoraddition, skalare Multiplikation, Lineare Unabhängigkeit von Vektoren

veröffentlicht am 04.12.2020

Wie wir gesehen haben, ist die Definition eines Vektors sinnvoll. Wenn wir aber Vektoren haben, dann stellt sich dieselbe Frage, wie bei Matrizen. Kann man mit diesen Vektoren sinnvoll rechnen?

Bei Matrizen haben wir bei der Vektoraddition einfach komponentenweise addiert:

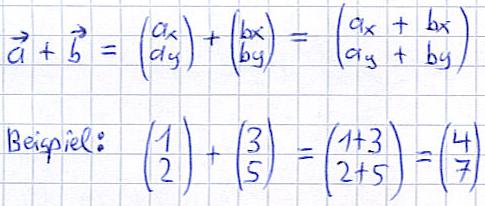
Aber macht das auch grafisch Sinn? Dazu haben wir uns folgende Überlegungen gemacht:

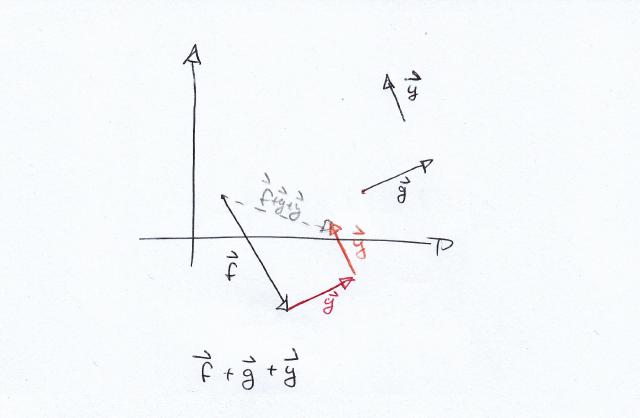
Die Vektoren f, g und y sind ja nicht ortsgebunden, daher können Sie einfach verschoben werden. Wenn man die Pfeile so verschiebt, dass Ende des einen der Anfang des nächsten ist, dann ist die gestrichelte Linie die Summe der drei Vektoren.

Die Vektoraddition ist sinnvoll definiert und sogar auch kommutativ. Das bedeutet, dass die Reihenfolge der Addition von Vektoren keine Rolle spielt. (man mag sich das gerne mal an obigem Beispiel überlegen)

Wem das nicht klar ist, der kann hier mal sich das erklären lassen:

externer Link: [mathebibel - Vektoraddition]

Ein Vektor kann aber auch mit einer reellen Zahl multipliziert werden. Man nennt das eine skalare Multiplikation,

De facto entspricht das nur einer "Vervielfachung" des Vektors. Das bedeutet, seine Länge wird geändert, aber nicht seine Richtung. Mit Hilfe der skalaren Multiplikation kann man also einen Vektor stauchen (Faktor betragsmäßig kleiner als 1) oder strecken (Faktor >1) oder sogar umdrehen (Faktor negativ)

Wenn man jetzt Vektoren mit Zahlen (Skalaren) multiplizieren kann und die Dinger auch noch addieren kann, dann erhält man eine Linearkombination von Vektoren.

Das entspricht dann einer "Verkettung von Vektoren". Vorwärts ist das ganz einfach, weil man die Vektoren ja einfach addieren kann. Eine Erklärung gibts auch nochmal hier

externer Link: [mathebibel - Linearkombination]

Darstellen von einem Vektor durch andere Vektoren

Wenn wir das obige aber umdrehen, dann wird es schon etwas komplizierter. Wir können mehrere Vektoren addieren. Toll.

Aber wenn wir einen Vektor vorgegeben haben, lässt sich dieser dann mit den anderen Vektoren herstellen?

Wie wir sehen, können wir damit der Vektor d durch die anderen mit geeigneten Skalaren x,y,z dargestellt werden kann.

Lineare Unabhängigkeit von Vektoren

Wenn wir mehrere Vektoren haben, dann will man manchmal wissen, ob alle Vektoren in "unterschiedliche Richtungen" zeigen, oder ob vielleicht zwei Vektoren eigentlich in dieselbe Richtung zeigen.

Wenn die Vektoren alle "wirklich" unterschiedlich sind, dann spricht man von linearer Unabhängigkeit.

Definition:

Mehrere Vektoren sind untereinander linear unabhängig, wenn keiner der Vektoren sich durch die anderen darstellen lässt.

Wie überprüft man das? Ganz einfach, man stellt ein LGS auf. Dabei entsteht ein LGS(3), welches weniger als 3 Variablen besitzt. Dies nennt man dann ein Überbestimmtes LGS (ÜLGS).

Bei ÜLGS Gleichungssystemen gilt, dass es entweder genau eine, oder keine Lösung geben kann

Warum ist lineare Unabhängigkeit wichtig?

Wenn wir uns einen dreidimensionalen Raum vorstellen, dass wird dieser von drei "Achsen" bestimmt. Nämlich von der x-, y- und z-Achse. Aber ein dreidimensionaler Raum entsteht auch, wenn man beispielsweise die Vektoren u,v, n nimmt: HIER FEHLT WAS

Wenn man jedoch die folgenden Vektoren a, b, c nimmt, dann entsteht KEIN dreidimensionaler Raum.

Warum? Ganz einfach, weil Vektor c in derselben "Ebene" liegt, wie a und b.

Wenn man also drei unabhängige Vektoren hat, dann zeigen diese "Pfeile" sozusagen in unterschiedliche Richtungen und "spannen" dadurch einen Raum auf. Genauso können zwei linear unabhänige Vektoren eine Ebene aufspannen.

Wenn zwei Vektoren sich nur durch einen skalaren Faktor unterscheiden, dann spricht man von Kollinearität. Bei Vektoren, die in einer Ebene liegen, spricht man von Komplanarität. Diese Begriffe sind im Buch auf Seite 340 und 341 erklärt.

weiterführende Links zu diesen Begriffen findet man hier:

externer Link: [mathebibel - Kollinearität (Abhängig von zweidimensionalen Vektoren)]

externer Link: [mathebibel - Komplanarität (Abhängig von dreidimensionalen Vektoren)]

externer Link: [mathematik.net - Komplanare Vektoren]

Abgabetermin: 10.12.2020

Aufgabe:

Buch S. 344 Nr 15a, 17c, 19 und 20 über Logineo. Der Kurs wird in den nächsten Tagen dort eingerichtet.

CI81 - M Vektorbegriff, Ortsvektor, 3D-Zeichnen und Längenberechnungen

veröffentlicht am 27.11.2020

Den Einstieg in die Vektorrechnung haben wir über Wegbeschreibungen von einem Gebäude zum nächsten gemacht.

Dazu haben wir zunächst zwei- und dreidimensionale Wege erarbeitet.

[Infoblätter mit Grundlagen Definitionen]

Anschließend haben wir den Begriff des Vektors, Ortsvektor und Pfeil definiert. Dabei sind uns wieder Begriffe aus der Unterstufe (Repräsentant, etc.) begegnet.

Mit Hilfe von Ortsvektoren und Pfeilen lassen sich dreidimensionale Objekte beschreiben und mit Hilfe der Längenberechnung auch Strecken berechnen.

Genauso wie Matrizen miteinander addiert werden können, kann man dies auch mit Vektoren tun. Es gibt auch sinnvolle Anwendungen dafür, beispielsweise für Kräfteparallelogramme aus der Physik.

Abgabetermin: 03.12.2020

Aufgabe:

Buch S. 332 bis 339 lesen und

Buch S. 343 4a,c,f und 5c,g,f

CI81 - M Abschließende Übung + Zusammenfassung Stochastik

veröffentlicht am 19.11.2020

In der heutigen Stunde haben wir eine komplexe Übungsaufgabe berechnet:

Die Aufgabe lautete:

Verteilung von Fahrrädern (rot) an verschiedenen Stellen in einer Stadt (A, B, C, D):

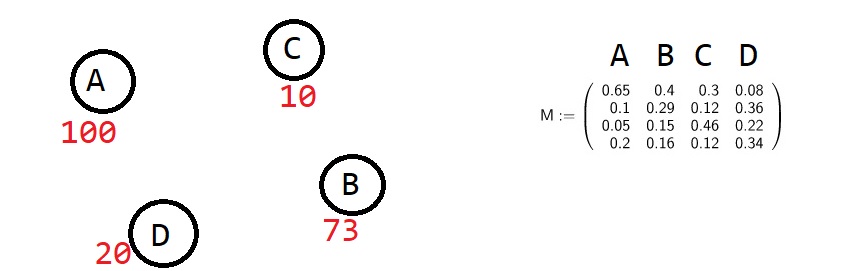
Die Anfangsverteilung kann aus dem Diagramm entnommen werden. Ebenfalls ist die Übergangsmatrix bereits angegeben.

Jetzt sollten die folgenden Aufgaben behandelt werden:

a) Wie viele Fahrräder befinden sich nach 1 Tag / 1 Woche an den verschiedenen Stellen in der Stadt?

b) Welche Anfangsverteilung würde sich bei derselben Wechselwahrscheinlichkeit invariant?

c) Wie lautet die stationäre Verteilung der gegebenen stochastischen Matrix?

Mit Geogebra lassen sich dann die folgenden Ergebnisse erzielen

Erklärung der einzelnen Rechenschritte:

1) Definition der stochastischen Matrix

2) Berechnung der Grenzmatrix durch Potenzieren (hier ^100) (Lösung zu c)

3) Berechnung der Verteilung nach einem Tag (Lösung zu a)

4) Berechnung der Verteilung nach 7 Tagen (Lösung zu a)

5) Aufstellen des LGS(4) für Berechnung des Fixvektors (Lösung zu b)

Abschließend habe ich noch die folgenden Übungsaufgaben zur Verfügung gestellt:

externer Link: [Mathebuch Prozesse - Leseprobe]

CI81 - M Berechnung des Fixvektors und Zusammenhang mit stationärer Verteilung

veröffentlicht am 13.11.2020

Wie wir in der letzten Einheit gesehen haben, kann es einen stationäre Verteilung geben. Diese lässt sich durch iteratives Multiplizieren / Potenzieren mit Hilfe von Geogebra sehr schnell berechnen.

Aber wie kann man das berechnen, wenn man keinen Rechner zur Verfügung hat?

Bevor wir uns mit diesem Problem beschäftigen, schauen wir uns ein ähnliches Problem an.

Exkurs: Fixvektor bei stochastischen Matrizen

Gegeben sei eine stochastische Matrix M. Angenommen wir hätten einen Vektor v bei dem folgendes gilt:

M*v=v

In diesem Fall ist das Verhalten ähnlich zu einer stationären Verteilung. Wir haben eine Verteilung auf unsere Zustände, die durch den Vektor v angegeben wird. Wenn wir unsere Übergangsmatrix darauf anwenden, dann passiert genau nix.

Das bedeutet, dass die Anzahl in den einzelnen Zuständen durch unsere Verteilung nicht geändert wird.

Definition:

Ein Vektor a wird als Fixvektor einer Markow-Kette bezeichnet, wenn gilt M*a=a

Offensichtlich ist das der Fall, wenn die Matrix M = der Einheitsmatrix ist. Dann wäre aber M eine absorbierende Matrix und es wäre vollkommen witzlos sich damit zu beschäftigen.

Also machen wir mal ein Beispiel:

Nehmen wir eine Übergangsmatrix, die wie folgt aussieht:

Preisfrage: Gibt es für diese Matrix einen Vektor v, so dass gilt M*v=v

Das bedeutet wir suchen einen Vektor mit der Eigenschaft eines Fixvektors. Das sieht dann so aus:

Wenn man M*v ausrechnet (siehe Multiplikation Matrix mit Vektor), dann sieht man mit etwas Fantasie , dass man daraus ein Gleichungssystem erstellen kann:

oha, das muss man doch lösen können, oder? Wenn Ihr das probiert, dann findet Ihr aber schnell heraus, dass das leider nicht so einfach geht. Es scheint irgendwie immer a=a oder b=b oder 0=0 herauszukommen.

Wie bestimmt man die Lösung eines LGS mit unendlich vielen Lösungen

Das lässt sich auch auf 3x3 Matrizen genauso übertragen. Dazu gibts Erklärungen in den folgenden Videos:

externer Link: [Youtube - mehrere Lösungen in einem LGS(3)]

externer Link: [Youtube - mehrere Lösungen LGS(3)]

Transfer: Berechnung des Fixvektors für ein konkretes Beispiel

Wie wir gesehen haben, kann man den Fixvektor bei bekannter Übergangsmatrix berechnen. Allerdings wird der Fixvektor in der Regel mit Parameter angegeben.

Berechnung des Fixvektors anhand der Übergangsmatrix

Beispielberechnung für die Gruppe 3 vom [Arbeitsblatt - Expertenpuzzle]:

Ergebnis

Damit haben wir den Fixvektor berechnet, es gilt also:

Berechnung des Fixvektors mit Berücksichtigung der Startverteilung

Laut Aufgabenstellung für dieses Arbeitsblatt sind die Kunden für jede Firma zu Beginn bekannt, das bedeutet in diesem konkreten Beispiel:

Das bedeutet mathematisch aber nichts anders als:

Damit ergibt sich jetzt aber ein Gleichungssystem mit einer zusätzlichen Gleichung:

Das kann man jetzt durch ein beliebiges Verfahren auf ein LGS(3) zurückführen und dieses Gleichungssystem hat tatsächlich eine eindeutige Lösung. Wenn man mehr Gleichungen als Variablen hat, dann gibt es eine eindeutige oder gar keine Lösung.

Wir zeigen hier mal die Lösung mit Geogebra:

Was haben denn die beiden Lösungen miteinander zu tun?

Das sehen wir hier:

Transfer: Zusammenhang Fixvektor und stationäre Verteilung

Wie wir gesehen haben, kann man den Fixvektor bei bekannter Übergangsmatrix berechnen. Allerdings wird der Fixvektor

So jetzt fertig mit dem Exkurs. Aber wofür nutzt uns das was? wir wollten doch eine stationäre Verteilung ausrechnen. Dafür schauen wir uns folgendes Beispiel mal an:

Das ist eine Markow-Kette (also eine stochastische Matrix). Wir suchen die stationäre Verteilung. Dazu schauen wir zunächst mit Geogebra an, was dabei herauskommt, wenn man M^100 rechnet, dann konvergiert ja M gegen die Grenzmatrix:

Wir können also die stationäre Verteilung in Zeile 9 erkennen.

Nehmen wir nun unsere Matrix und berechnen den Fixvektor mit der Methode B), das einzige was wir jetzt ändern ist, dass wir nicht die Startverteilung benutzen, sondern die Gleichung IV =1 ändern.

Dann erhalten wir mit Geogebra:

Die letzte Zeile nochmal als Kommazahlen und im Vergleich zur Grenzmatrix:

Na fällt was auf? Offensichtlich haben die Grenzmatrix und der Fixvektor etwas miteinander zu tun. Denn sie sind ja exakt gleich!

Fazit:

Wenn man eine stationäre Verteilung sucht, dann hat man auch den Fixvektor berechnet. Umgekehrt gilt genauso, wenn man den Fixvektor berechnet, dann kann man daraus die stationäre Verteilung bestimmen.

Das führt zu folgenden "Kochrezepten:

Berechnung der stationären Verteilung

Wenn wir eine Markow-Kette haben, die eine stationäre Verteilung besitzt, dann kann man die Grenzmatrix (stationäre Verteilung) berechnen, indem man zuerst den Fixvektor mit der Zusatzgleichung (a+b+c=1) berechnet.

Der Fixvektor entsprechend häufig nebeneinander ergibt die stationäre Verteilung

Interpretation / Bedeutung:

Wenn man die Übergangsmatrix immer und immer wieder anwendet (also beliebig viele Schritte in Richtung "Zukunft" geht, d.h. M^n) dann konvergiert die Matrix M gegen diese Grenzmatrix G.

Berechnung des Fixvektors bei gegebener Startverteilung

Wenn wir eine Markow-Kette haben, dann kann man den Fixvektor mit der Zusatzgleichung (a+b+c=Summe_aller_Werte_der_Startverteilung) berechnen.

Dieser Fixvektor hängt natürlich von der Startverteilung ab und gibt an, welche Startverteilung sich unter der gegebenen Markow-Kette nicht ändern würde.

Interpretation / Bedeutung:

Das bedeutet, dass wenn die Verteilung so ist, wie in dem Vektor angegeben, dann ändern sich diese Werte bei Anwendung der Übergangsmatrix nicht mehr.

Abgabetermin: keiner

Aufgabe:

keine, denn ich habe für diesen Artikel ca. 3h gebraucht. Jetzt habe ich keinen Bock mehr mir eine Aufgabe auszudenken.

CI81 - M Markow-Kette, absorbierende Zustände und stationäre Verteilung

veröffentlicht am 12.11.2020

Nachdem wir uns jetzt mit den verschiedenen Anwendungen von stochastischen Matrizen beschäftigt haben (bspw. Berechnung zukünftiger Verteilungen) fehlen uns noch ein paar Besonderheiten und Begriffe.

Markow-Ketten

Definition:

Ein stochastischer Prozess der mit Hilfe einer Übergangsmatrix dargestellt werden kann heißt Markow-Kette.

Das ist jetzt einfach ein neuer Begriff anstelle einer "stochastischen Matrix". Beide besagen prinzipiell dasselbe.

externer Link: [Youtube - Jung: Markow-Kette]

Absorbierende Zustände

Bei der Betrachtung einer Markow-Kette (in diesem Fall eines Ausbildungssystems) kann es passieren, dass Zustände erreicht werden, aber diese nicht mehr verlassen werden. Zur Begriffssicherung haben wir folgendes Beispiel:

Hier kann man erkennen, dass in manchen Spalten der Übergangsmatrix nur eine 1 auftaucht und sonst nur Nullen. Das bedeutet, dass dieser Zustand zwar erreicht werden kann, aber dieser Zustand nie wieder verlassen wird.

Definition:

Einen Zustand, der nie wieder verlassen werden kann, bezeichnet man als absorbierender Zustand.

Definition:

Eine stochastische Matrix heißt absorbierende Markowkette, wenn sie mindestens eine Spalte mit exakt einer 1 und sonst nur Nullen enthält.

Das bedeutet praktisch: Stellen wir uns Kugeln vor, die in den einzelnen Behältern(Zustände) liegen und dann gemäß unserer Übergangsmatrix von einem Behälter (Zustand) in einen anderen Behälter wechseln.
Es gibt dann einen "absorbierenden" Behälter, aus dem werden nie wieder Kugeln herausgenommen. Das bedeutet, im Laufe der Zeit sammeln sich alle Kugeln in diesen "absorbierenden" Behältern an.

externer Link: [Youtube - Jung: Absorptionswahrscheinlichkeiten bei Markowketten]

Stationäre Verteilung

Wenn man das Beispiel der Gruppe Nr 2 von dem Arbeitsblatt afasdfa nimmt, dann stand unter Aufgabe ... ja, man solle folgendes berechnen:

A^10, A^20 usw. Das haben wir mal getan und dazu die Software Geogebra verwendet. Das Ergebnis sieht dann so aus:

[Bild Screenshot Verteilungen]

Wie man sehen kann, ändert sich die enststehende Matrix nicht weiter. Damit kann man auf die Vermutung kommen, es existiert ein Grenzwert dieser Matrix.

Denselben Effekt kann man sich hier auch nochmal erklären lassen:

externer Link: [Youtube - Jung Grenzmatrix]

Das führt dann zu folgender Begrifflichkeit:

Definition:

Wenn eine stochastische Matrix bei wiederholter Multiplikation mit sich selbst einen Grenzwert hat, dann spricht man von einer stationären Verteilung.

zugehöriger Tafelshot (rechte Seite der Tafel)

CI81 - M Inverse Matrix berechnen und Anwendungen auf stochastische Matrizen

veröffentlicht am 30.10.2020

Beim Matrizenrechnen gibt es auch eine Gruppe bezüglich der Verknüpfung "Multiplikation". Das bedeutet es gibt ein neutrales Elementf bei der Multiplikation und auch für jedes Element ein Inverses.

Bei Matrizen ist das neutrale Element die sogenannte Einheitsmatrix.

Wenn man eine beliebige Matrix gegeben hat, dann will man wissen, mit wie die zugehörige Inverse Matrix aussieht:

und die zugehörige Inverse Matrix ist:

weil es gilt

jetzt ergibt sich ein Problem:

Wie berechnet man die Inverse Matrix?

bei dem obigen Beispiel taucht das wie aus heiterem Himmel (also wie von alleine) auf. Aber wie kann man das berechnen?

Es gibt verschiedene Rechenverfahren um die inverse Matrix zu berechnen. Für den Mensch ist die einfachste Form der "simultane" Algorithmus nach Gauß-Jordan. Dazu seien hier zwei Videos verlinkt:

externer Link: [Youtube - Inverse berechnen bei 2x2 Matrizen]

externer Link: [Youtube - Inverse berechnen bei 3x3 mit ausführlicher Erklärung]

Damit kann man nun die inverse Matrix berechnen. Ein paar Übungsaufgaben dazu findet Ihr hier:

externer Link: [Online Aufgaben zu Inverse berechnen]

zur Kontrolle könnte ihr auch das hier benutzen:

externer Link: [Inverse Matrix Rechner]

Ist die Menge der Matrizen mit der Matrixmultiplikation eine Gruppe?

Ja ist sie. (teilweise). Wir können nämlich eine Inverse nur dann berechnen, wenn die Matrix selber keine Nullzeilen oder Nullspalten (d.h. eine Zeile/Spalte voller Nullen) enthält.
Für unsere Schulmathematik reicht es also aus, dass für alle Matrizen (für Wißbegierige: deren Determinante <> 0 ist) es eine Inverse gibt.

Abgabetermin: 05.11.2020

Aufgabe:

Bitte bearbeitet Euer Arbeitsblatt zu Ende:

Download: [ausgeteilte Arbeitsblätter zur Anwendung stochastischer Matrizen]

CI81 - M Rechnen mit Matrizen, Gruppenbegriff

veröffentlicht am 29.10.2020

In der heutigen Stunde haben wir uns das Rechnen mit Matrizen genauer angeschaut. Die Menge der Matrizen bildet eine Gruppe. Die Eigenschaften einer Gruppe hatten wir schon mal in der Unterstufe behandelt:

Download - [Arbeitsblatt - Was ist eine Gruppe]

Also betrachten wir zunächst die einfache [+] Operation mit zwei Matrizen:

Das scheint ja schon sinnvoll zu sein. Es kommt offensichtlich wieder eine n x n Matrix raus.
Für die Gruppe müssen insgesamt 3 Dinge nachgewiesen werden:

Eigenschaften bei [+] Operation

G1) Nachweis Existenz eines neutralen Elementes bei [+] Operation

G2) Nachweis eines inversen Elements zu einem vorgegebenen beliebigen Element A aus M

G3) Nachweis der Assoziativität

Damit ist nachgewiesen, dass es sich um eine Gruppe handelt.

Eigenschaften bei [*] Operation

Übertragen des Beispiels auf die Multiplikation [*] Operation zwischen zwei Matrizen:

Zunächst sei die Festlegung, wie man genau multipliziert nochmal angegeben:

Das müssen wir erstmal üben:

Übungsaufgaben zur Matrizenmultiplikation:

externer Link: [Übungsaufgaben mit Kontrolle, enthält auch m x n Matrizen]

externer Link: [Multiplikation mit Matrizen, Erklärung + Aufgaben]

G1) Nachweis Existenz eines neutralen Elementes bei [*] Operation

Also gibt es mit der Einheitsmatrix offensichtlich ein neutrales Element. Denn es verändert bei Multiplikation nichts.

Abgabetermin: 30.10.2020

Aufgabe:

Bitte bearbeitet Aufgaben 1) bis 3) (siehe entsprechend Twitter Feed auf der rechten Seite:

Informiert bitte darüber, wie man die Inverse einer Matrix berechnen kann, dazu könnt Ihr folgenden Link verwenden:

externer Link: [Wie berechnet man die Inverse einer Matrix]

CI81 - M stochastische Matrix, Matrizenmultiplikation

Abgabetermin: keiner

Zwischen verschiedenen Darstellungen (Text <-> Übergangsdiagramm <-> Übergangstabelle <-> Übergangsmatrix) kann man beliebig hin und herwechseln. Ein zugehöriges Übungsblatt haben wir im Unterricht behandelt:

[Arbeitsblatt Darstellungswechsel]

Von Übergangsmatrizen zu allgemeinen Matrizen

Eine Übergangsmatrix [Definition lt. Wikipedia] ist eine spezielle Form einer allgemeinen Matrix. Eine Matrix besteht aus Zeilen und Spalten und enthält an jeder Position einen Wert.

externer Link: [Definition einer allgemeinen Matrix gem. Wikipedia]

Das sieht dann so aus:

Rechnen mit Matrizen

Wir beschäftigen uns in der Schule nur mit quadratischen Matrizen, das heißt die Anzahl Zeilen und Spalten sind gleich. Beispiele für Matrizen sind:

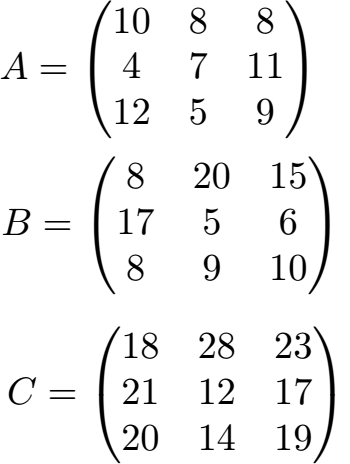
Wenn man Matrizen definiert hat, stellt sich die Frage, kann man damit rechnen? Ja man kann.

Für unsere Zwecke benötigen wir eine Definition, wie eine Multiplikation ausgeführt werden kann. Dabei ist es wichtig, dass nach der Durchführung der Multiplikation wieder eine quadratische Matrix herauskommt.

Die Multiplikation von zwei Matrizen ist wie folgt festgelegt:

Für das manuelle Rechnen kann man folgendes Verfahren sich leicht merken:

externer Link: [Erklärung des Rechenverfahrens anhand von 2x2 Matrizen]

externer Link: [Youtube - Erklärung der Multiplikation mit 3x3 Matrizen]

neutrales Element bei der Matrixmultiplikation

Bei der normalen Multiplikation gibt es die 1. Diese ist "neutral", weil 5*1=5 ist. Bei der Matrixmultiplikation gibt es auch ein neutrales Element und zwar die Einheitsmatrix. Hier sind die Einheitsmatrizen für 1x1, 2x2, 3x3 und 4x4 Matrizen dargestellt.

$I_{1}={\begin{pmatrix}1\end{pmatrix}},\ I_{2}={\begin{pmatrix}1&0\\0&1\end{pmatrix}},\ I_{3}={\begin{pmatrix}1&0&0\\0&1&0\\0&0&1\end{pmatrix}},\ I_{4}={\begin{pmatrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{pmatrix}}$

Man sieht also, die Einheitsmatrix (also das neutrale Element bzgl. der oben definierten Matrixmultiplikation) sieht immer so aus, dass auf der Diagonalen lauter 1en stehen.

Weitere Informationen zu Matrixmultiplikation findet Ihr hier:

externer Link: [SimpleClub - Was sind Matrizen]

externer Link: [Youtube - Taschenrechner Bedienung Matrixmultiplikation]

CI81 - M Einstieg in stochastische Prozesse

Abgabetermin: 08.10.2020

Wir kennen aus AE2 bereits State-Machines. Diese State-Machines kann man gut zur Visualierung von Abläufen verwenden.

Wir haben heute uns mit einer Mustererkennung beschäftigt. Das könnte z.B. so aussehen:

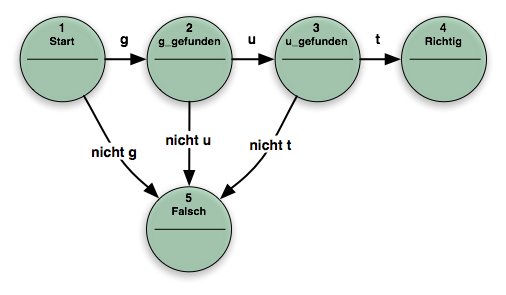
(Quelle: Wikipedia-Artikel zu Endlichen Automaten)

Bei der Mustererkennung hat man aber das Problem, dass nicht immer ein Buchstabe tatsächlich gefunden wird. Manchmal erkennt man ihn und manchmal nicht. Warum das so ist, dass steht in dem Infoblatt:

[Infoblatt zu Mustererkennung und Problemen dabei]

Daher lässt sich der Übergang von 1 zu 2 bzw von 1 zu 5 mit Wahrscheinlichkeiten angeben.

Beispielsweise: Zu 70% wird ein Buchstabe erkannt und zu 30% klappt das halt nicht. Dadurch ergibt sich ein sogenannter stochastischer Prozess. Das haben wir in folgendem Tafelbild festgehalten:

In diesem Tafelshot sehen wir noch eine zugehörige Übergangsmatrix. Die Herleitung der Übergangsmatrix kann mit folgendem Arbeitsblatt leicht erarbeitet werden

[Arbeitsblatt: Übergangsdiagramme und Übergangsmatrizen]

Diese Erkenntnisse kann man jetzt nutzen, um beispielsweise für eine Schulmensa die notwendigen Essen zu berechnen.

Einen solchen Vorgang nennt man auf eine Markow-Kette.

weiterführende Links:

externer Link: [Website - sämtliche Inhalte auf einer Website]

Aufgabe:

Bitte bearbeitet Aufgaben a-c auf der ersten Seite von diesem Arbeitsblatt:

[stochastischer Prozess bei Übergangsmatrizen]

Wiederholt bitt ebenfalls die Begriffe: "Gruppe", "neutrales Element" und "inverses Element bzgl einer Verknüpfung"

Die Seite 2 und die zugehörigen Aufgaben besprechen wir nächste Woche.

CI81 - M Download Software für Stochastik

Abgabetermin: keiner

Sowohl im Tauschverzeichnis der Schule, als auch hier findet Ihr jetzt die Software, welche die Schule für Euch lizensiert hat.

Damit könnt Ihr Euch (mit einer zugegeben schlechten Oberfläche) selber Übungsaufgaben und Erklärungen rund um das Thema Stochastik erarbeiten.

Wir benötigen nur die Module für Baumdiagramme und für Kombinatorik. Wir werden keine Zufallsvariablen und Binomialverteilungen machen.

[Download Stochastik Teil 1 - Software]

[Download Stochastik Teil 2 - Software]

CI81 - M Kombinatorik

Abgabetermin: 01.10.2020

Heute haben wir uns mit mehrstufigen Zufallsexperimenten beschäftigt. Dabei haben wir die beiden Pfadregeln zum Berechnen der Wahrscheinlichkeiten in einem Baum besprochen.

Die entsprechenden Inhalte findet man im Buch auf Seite 104 und 105.

Eine einfache Erläuterung dieser Pfadregeln kann man auch sich hier nochmal anschauen:

externer Link: [Pfadregeln in einem Baum]

externer Link: [Youtube - Baumdiagramme allgemein]

externer Link: [Youtube - Pfadregeln in einem Baum]

externer Link: [Youtube - 1. und 2. Pfadregel]

Nachdem man sich mit der Wahrscheinlichkeitsberechnung in einem Baum beschäftigt hat, kommt ein typisches Problem:

Man muss zunächst einmal die Anzahl Elemente in der Ergebnismenge OMEGA und die Anzahl Elemente der Ereignismenge bestimmen.

Im Unterricht (siehe entsprechendes Tafelbild bei Twitter) haben wir zwei recht ähnlich lautende Ereignisse behandelt. Der Unterschied der beiden Ereignisse bestand darin, dass bei einem der beiden die Reihenfolge der Ergebnisse entscheiden war, bei dem anderen jedoch nicht.

Davon hängt aber ab, wieviele Ergebnisse überhaupt gezählt werden müssen. Dies führt zu sogenannten

"Zählstrategien"

Im Buch findet man diesen Inhalt auf Seite 109 bis 113.

Als Zählstrategie bezeichnet man das Zählen von Ergebnissen, die überhaupt nur auftreten können. Man bezeichnet dies auch als

"Kombinatorik"

Die folgenden Links sollen Euch helfen, Euch die vier möglichen Zählstrategien zu erarbeiten und zu verstehen.

externer Link: [Youtube - Kombinatorik Song]

externer Link: [Youtube - Zählstrategien Beispiele]

externer Link: [Youtube - Fakultät erklärt (auch Permutationen)]

externer Link: [Youtube - alle vier Zählstrategien mit Donuts]

Aufgabe:

Bitte bearbeitet

◦ Lesen Buch S. 110 bis 113
◦ alle Übungsaufgaben auf Seite 110 bis 113, die Lösungen zu diesen Aufgaben findet Ihr hinten im Buch.

In der nächsten Woche werden wir dann noch eine komplette Doppelstunde mit Zählstrategien beschäftigen.

CI81 - M Inhaltsübersicht Klassenarbeit

Abgabetermin: keiner

Der Vollständigkeit halber liste ich mal die Inhalte der Mittelstufe nochmal auf, damit man nachschauen kann, ob bei der Vorbereitung für morgen man alles berücksichtigt hat.

Ableitungen bestimmen
Ableitungsregeln (KR, QR, PR) kennen
Extrema und Wendepunkte bestimmen
Funktionsgleichungen bestimmen können
Integralrechnung

mehr war es eigentlich nicht. Unten habe ich noch ein paar Links ergänzt.

Viel Erfolg morgen.

CI81 - M Flächenberechnung zwischen Graph und x-Achse

Abgabetermin: keiner

Wir haben heute die Flächenberechnung zwischen zwei Funktionen besprochen. Das ähnelt eigentlich der Berechnung zwischen x-Achse und Graph. Aber es ist sogar noch etwas einfacher:

Vorgehen zur Bestimmung der Fläche zwischen zwei Funktionen:

Schnittpunkte von f(x) und g(x) bestimmen
Grenzen festlegen, ggfs in Teilintervalle zerlegen
Integral der Differenz-Funktion (f(x)-g(x)) bilden. Dabei darauf achten, welche Funktion "oben" ist.

Die Fläche zwischen zwei Funktionen wird auch hier erklärt:

externer Link: [Youtube: Berechnung von Flächen zwischen zwei Funktionen]

externer Link: [Youtube: Fläche zwischen Funktionen auf die coole Art]

externer Link: [Flächenberechnung mit Text und Beispiel]

Das Beispiel aus dem Unterricht (Buch S.318 Nr 3) war sehr schwierig, daher habe ich die komplette Lösung mal als Video gestreamt. Ebenfalls habe ich ein ähnliches Video (mit wesentlich leichterer Aufgabe) verlinkt.

externer Link: [Twitch: Videoerklärung der Aufgabe Buch S.318 Nr 3, Feuerwehrlöschteich]

externer Link: [Youtube: Grenze bestimmen, wenn Integralwert bekannt]

Empfehlung:

Im Buch findet Ihr auf den Seiten

Buch S. 313 bis 316
Buch S. 317f bietet nochmal einen Überblick über die Einheitenbildung

gute Beispiele und Erklärungen zur Berechnung von einfachen Integralen/Flächen.

Als Transferaufgabe und als Vorbereitung auf die Klassenarbeit solltet Ihr folgende Aufgabe downloaden:

[Übungsaufgabe zu Extrema, Wendesstellen und Flächenberechnung]

Die Aufgaben a) bis e) sind geeignet um sich auf die KA vorzubereiten.

CI81 - M Flächenberechnung zwischen Graph und x-Achse

Abgabetermin: 03.09.2020

Wir haben heute die Flächenberechnung zwischen x-Achse und Graph besprochen. Wichtig ist dabei das Vorgehen:

Nullstellen bestimmen
Grenzen festlegen, ggfs in Teilintervalle zerlegen
Einzelne Integrale berechnen und die Beträge davon addieren

Als weitere Quellen für die Flächenberechnung habe ich folgende Erklärvideos herausgesucht:

externer Link [Twitch: digitale U-Stunde Flächenberechnung zwischen x-Achse und Graph]

externer Link [Youtube Video: Flächenberechnung zwischen x-Achse und Graph]

externer Link [Website mit Erklärung der Integralrechnung]

Aufgabe:

Bitte bearbeitet

◦ Buch S. 312 Nr 2 i, l
◦ Buch S. 311 Lupe 5 lesen und Aufgabe b darunter (Lösung steht hinten im Buch)

verwendet auch Geogebra um Eure Ergebnisse zu kontrollieren und eine bessere Vorstellung davon zu bekommen. Abgabe ist zunächst für nächste Woche Donnerstag im Präsenzunterricht geplant. Falls sich was ändert, melde ich mich per Mail bei Euch.